上一篇聊了事後檢定跟型一型二誤差之後，
接下來我想聊聊相關，下一篇聊迴歸和機器學習：）

之前的討論大多聚焦於單樣本檢定或是實驗操作的檢定，
那萬一今天有一件事情是不能做實驗去操作的怎麼辦？

像是，我們常常聽到刻板印象說，
男生比較擅長讀理工科，所以理工科男生比女生多。

這句話實際上我們是無法去用實驗來驗證的，
因為實驗的情境需要控制所以其他可能會影響的變因，
而我們又不可能變出兩組完全不受其他社會因素影響，
只有性別有差的受試者，來實驗說他們是不是比較擅長理工科。
更無法測試說，假設男生女生一樣擅長理工科，
理工科的男生女生就會一樣多。
所以上面那個刻板印象的敘述，
基本上是無法有科學證據支持的。

但是那句描述其實是在說一個「相關」的關係，
也就是理工科系的性別比，男生可能普遍比女生多。
這裡科系裡的「性別」跟「數量」是「相關」的，
但「性別」本身卻不一定是造成這個現象的原因。
造成這個現象的原因有可能是性別文化
（例如預設女生就是做不好的這種文化，
本身就會讓更多女生不想來念這個科系。）
或社會風氣（覺得女生應該長怎麼樣子，
所以念理工科是很奇怪的），
而不是性別本身有天生的差異。

那句刻板印象，基本上是「把相關當成因果」，
這是統計上面很大的一個偏誤。
雖然兩件事情有因果關係，
保證兩者之間一定有相關關係，
但反過來卻不一定成立。
有相關關係的兩件事情A和B，
他們之間的關係可能是：

1. A是因，B是果
2. B是因，A是果
3. A跟B都是某個不存在討論之中的變數C的果
4. A跟B之間的因果關係會受變數C調節改變

但不幸的是在研究人類相關的行為或是現象上，
我們很多時候是只能研究到相關，
無法進一步做實驗去推出是否為因果關係。

然而這樣子的偏誤，在現實中無所不在。
比如說有人覺得比爾蓋茲大學中輟，
後來有了微軟，成為成功的創業家，
就覺得要創業成功一定要中輟才可以。
但是他的中輟跟他的成功只是相關關係，
不中輟就成功的創業家也很多，
中輟然後創業失敗的人更多，
這就是把相關當因果。

除了上面的例子，
還有很多其他生活之中的例子。
例如說我在美國辦汽車保險的時候，
有一個問題是我讀什麼學校。
然後因為我讀的學校很不錯，
所以我另外得到了一個「好學生折扣」。

這個東西怎麼來的呢？
可能過往他們的資料顯示，
讀比較好的學校的學生，
開車出事的機率較低。
所以他們就拿這個來設計保費費率。
這個原因可能是好的學校的學生有比較多資源，
不需要在開車打工到很晚之類的。
或者是好學校的學生有比較多資源買車，
不會去買二手爛車，增加出事率。
（這只是我的猜測，沒有實證。）

但問題是，
我讀的學校好不好跟我會不會出車禍有啥關係？
我也可以讀很好的學校但我很愛飆車，
或是我讀很差的學校但我很注意開車安全。
這兩件事情其實不是直接相連的，
卻因為存在相關關係，就被當成因果。
這樣其實還會造成很多後續連鎖效應，
比如說因為比較好的學校的學生可能負擔不起好的保險，
所以他們的保額可能就比較低，甚至是很多不給付，
在他們出事的時候，能得到的協助就很少，
他們可能就得把車賣掉買更爛的車，
接著惡性循環下去。

這件事情寫在這裡，希望大家稍微能有點感覺，
把相關當因果可能會產生各種各樣的問題。

但不幸的是，現在大家耳熟能詳的機器學習，
很常是立足在這樣子的基礎上的。

在細說那部分之前，
我們這篇先回頭介紹一下描述相關關係的「相關係數」，
以及下一篇再介紹其延伸的「迴歸(Regression)」，
然後才開始談機器學習。

要說明相關，我們先看看以下的圖：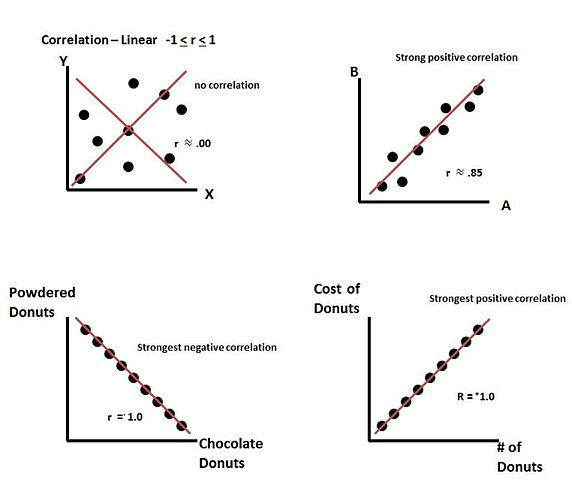

（圖片來源：https://commons.wikimedia.org/wiki/File:Correlation_coefficient.png）

相關係數的概念，就是去描述說，
一群資料點，在兩個變數之間的關係，
是不是能夠用一條線去描述。

像上面的圖裡面r=1跟指的就是高度正相關的情況，
也就是存在一條線，能夠完美通過所有資料點，
且斜率是正的。
這翻成白話文，就是在說這兩個變數之間，
如果一個增加了，另一個也會等比例增加。
反過來如果是r=-1，則是高度負相關，
也就是如果一個變數增加了，另一個會等比減少。
如果兩者之間沒有相關，r接近為零，
那我們說這兩個變數間沒有相關。
在實務研究上，
我們把相關程度大於0.7稱為高度相關，
大於0.3小於0.7稱為中度相關，
小於0.3就是低相關，甚至考慮成沒有相關。

有了這個基本概念，下一篇我們就來談迴歸，
以及迴歸的概念怎麼推廣到機器學習的基礎。

敬請期待（？